Monotonicity: Find the K-th number in two sorted arrays
Given two sorted arrays of integers, $A$ and $B$, find the $K$-th smallest integer from A and B in $O(\min(\log{N}, \log{M}))$ time. $N$ and $M$ are the size of $A$ and $B$ respectively.
Without loss of generality, we can assume A and B are of the same length N. Because
both A and B are sorted, we can merge A and B into a sorted array C in $O(N)$ and the answer
would be C[K-1]. We can stop when there are K elements in C, so the time
complexity is $O(K)$. Can we do better?
Yes. Of those final K numbers merged into C,
some are from A, others are from B. If there is an oracle that tells us, i numbers are
from A, then we know the answer is max(A[i-1], B[K-i-1]). The approach above essentially
enumerates i from 1 to N. Can we do better?
Yes. The insight is that i exhibits monotonicity. Let's say we try any value i, we know how many
numbers in B are less than or equal to A[i-1], say j. If i+j < K, we know we should select
more than i numbers from A. Otherwise, we know we must select no more than i numbers from A.
This monotonicity means we can binary search $i$ in $O(\log{N})$. Are we there?
No. For each i, finding j requires $O(\log{N})$ itself. In total, the time complexity
is $O((\log{N})^2)$. We can improve this approach by shrinking the size of the problem.
After a check of i, we have knowledge of which part of A and B to look at.
For example, if i+j < K,
shrink the problem to: Find the K-(i+j)-th number in A[i:N] and B[j:N].
Otherwise, shrink the problem to: Find the K-th number in A[0:i] and B[0:j].
It gets complicated to analyze the exact time complexity. However, it is obvious that
it is more than $O(\log{N})$. Can we do better?
Yes. Given i, we know we need to pick K-i numbers from B.
In order to make sure i is the answer, we must make sure numbers we select from A and B are
indeed the smallest K numbers. That translates to the following two conditions.
- Remaining numbers in A are larger than or equal to B[K-i-1], i.e., $B[K-i-1] \le A[i]$.
- Remaining numbers in B are larger than or equal to A[i-1], i.e., $A[i-1] \le B[K-i]$.
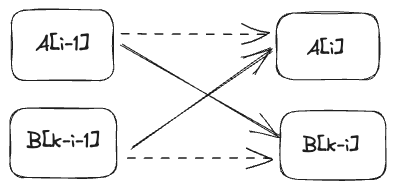
The head of arrow is larger than or equal to the tail. The dashed arrows represent the problem definition that A and B are sorted. The solid arrows represent conditions we check.
Here is the implementation and test in Go.
1func FindKthNumberInTwoSortedArrays(a, b []int, k int) int {
2 n, m := len(a), len(b)
3 if n > m {
4 n, m = m, n
5 a, b = b, a
6 }
7
8 // Handle special cases for code readability.
9 // Case 1. use 0 number from a
10 if k <= m && a[0] >= b[k-1] {
11 return b[k-1]
12 }
13 // Case 2. use 0 numbers from b
14 if k <= n && b[0] >= a[k-1] {
15 return a[k-1]
16 }
17
18 // Case 3. use some numbers from a and b.
19 low, high := 1, min(k-1, n)
20 for low < high {
21 // use i numbers in a.
22 i := (low + high) / 2
23 j := k - i
24 if j < 0 || (j < m && a[i-1] > b[j]) {
25 high = i - 1
26 continue
27 }
28 if j > m || (i < n && j > 0 && b[j-1] > a[i]) {
29 low = i + 1
30 continue
31 }
32 low = i
33 break
34 }
35
36 if k-low-1 >= 0 {
37 return max(a[low-1], b[k-low-1])
38 }
39 return a[low-1]
40}
Practice online at Leetcode 4. Median of Two Sorted Arrays